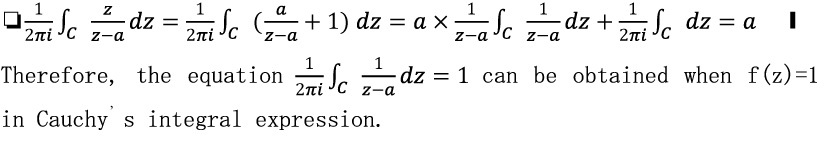✝Encounter with Möbius Inversion: f(z)=1/z
Let’s go back to my testimony.
In the preface of the textbook on complex Analysis, which I took in my hands, it was written as follows.
-Although Real Numbers are sufficient to describe the visible World, we need Complex Numbers to describe the invisible World i.e. the supermicroscopic world composed of elementary particles.
Intrigued by the preface, I opened the book and…
I was really astonished to find there an explanation about the function called Mbius Inversion or Complex Inversion.
First of all, I want to tell you how great (even ground-breaking) this function is. -It looked to me like the basic blueprint of the World.
Just try to imagine how enormous my astonishment and excitement were!
I’m going to describe it as simply as possible, but I can’t avoid mathematical formulas. I’d like you to agree with it.
Moreover, it took me more than 1 year to reach the following understandings, but I show them all at once in a condensed manner.
-Mbius Inversion or Complex Inversion is a very simple function which can be described as xy=1.
When both of x(z) and y(z’) are real numbers, it gives us a graph of hyperbola.
When both of them are Complex Numbers, however, it represents the operation to exchange inside and outside of the unit circle (whose radius is 1): f(z)=1/z. x(z).
Hence, x(z) and y(z’) are always positioned separately inside and outside of the unit circle.
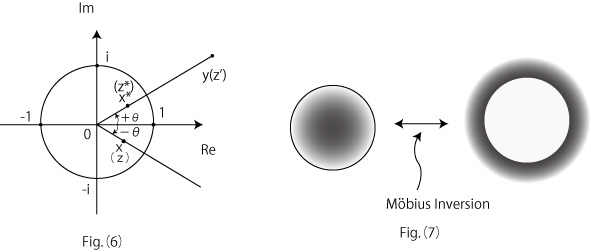
Note) x∗(z∗) is called the complex conjugate of x(z).
-When z=a+bi, z∗=a-bi(a,b: real numbers). With x and y exchanged(x↔y), it means the same thing. We usually use z and z’ instead of x and y.
Möbius Inversion is generally described as z’=1/z or f(z)=1/z.
z’ and z∗ are said to be in `mirror image’ relationship.
It is amazing!! -I clapped on my knees in spite of myself.
For I instantly got the inspiration (conviction actually) that the inside and the outside of the circle correspond to Consciousness and Unconsciousness of human mind.
-I mean there must be the exact correspondence between the two facts: that the inside and the outside together make up the whole Complex Plane and that Consciousness and Unconsciousness together make up the whole human existence.
This is what Lacan said!! Isn’t Complex Inversion(f(z)=1) the Möbius Strip itself, which he kept in mind throughout his life as model of human existence?
For the inside and the outside of Complex Inversion correspond exactly to the front and the back of the Möbius Strip.

Anyway…
If a textbook of natural science refers to this function, doesn’t it mean that we can adapt Complex Inversion to everything in Nature?
Actually, didn’t its preface talk about the World of elementary particles?
I couldn’t control my excitement.
While I was reading the textbook further, I encountered Complex Integration of Complex Inversion※, which was full of profound and mysterious suggestions.
※We call it Mbius Integration in this book.
Before pushing my testimony further, I’d like to introduce basic knowledge about Complex Function and Complex Integration.
※Complex Function is expansion of Real Function, which we learned
at high school(y=f(x)).
The former is obtained by expanding variables from real to complex(x,y→z) .
For example, f(z)=(z-a)n corresponds to f(x)=(x-a)n, sinz to sinx.



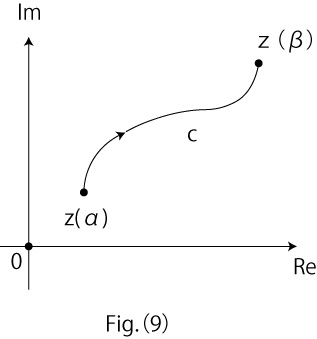
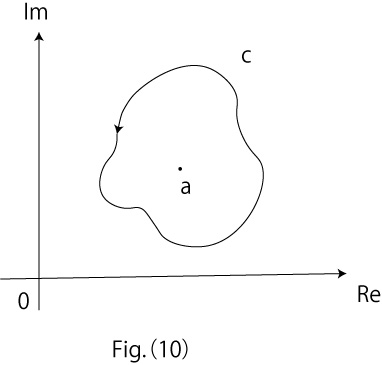
※The integration value of a complex function is defined as line integral along a closed curve C on the complex plane, as indicated in the Fig.(9).
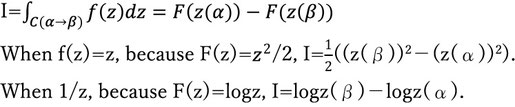
※When we integrate a complex function along a closed curve C, very interesting phenomena occur, which phenomena we can’t see with real functions.
Here, I’d like to refer to the notions of Regular and Non-regular about complex functions.

Anyway, the expression above is very rough, because we have a strict definition of Regular and Non-Regular complex functions.
Nonetheless, when Regular complex functions are concerned, you can think of them as those other than Complex Inversion without any serious problems (at least in this book).
※It is not too much to say that the proposition below is the essence of Complex Integral Calculus.

From now on, we are going to watch closely this proposition, which is both interesting and mysterious.
I kept on struggling with mathematical formulas while I forgot about the time. I wonder how many hours I stayed before the bookshelf…
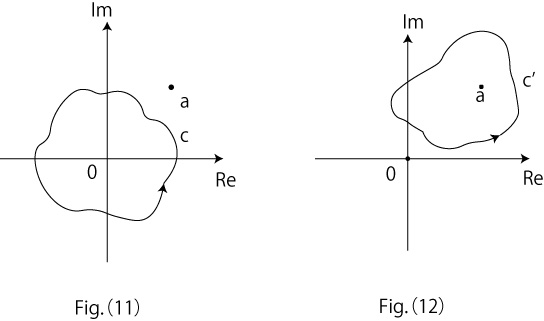
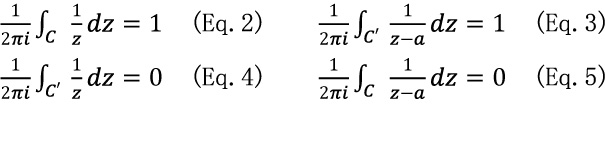
Fig.(11),Fig.(12);(Eq.2),(Eq.3),(Eq.4),(Eq.5) mean the following:

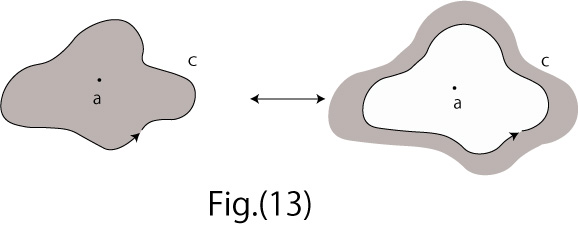
Fig.(13) and Eq.3 represent the operation to make difference between the `inside’ and the `outside’ of closed curve C surrounding the fixed point a (singularity) ; it is an expanded notion of Complex Inversion already mentioned.
It means that Mbius Integral represents the operation to exchange the `inside’ with the `outside’ of any closed curve C.
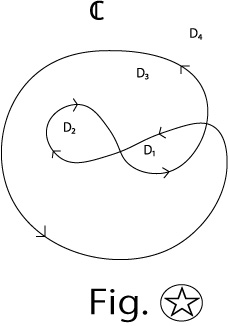
Here, I’d like you to notice that there is no condition about the shape of the closed curve C; for example, Eq.3 holds also about a curve like ℭ.
By the way, a closed curve like C which has no intersection points within itself is called a Jordan closed curve, and one like ℭ which has intersection points within itself a general closed curve.
The Inside of ℭ corresponds to D1∪D3 and Outside to D2∪D4 .
If we expand the discussion above and show its relationship with Set Theory, we obtain the following figures and equations.
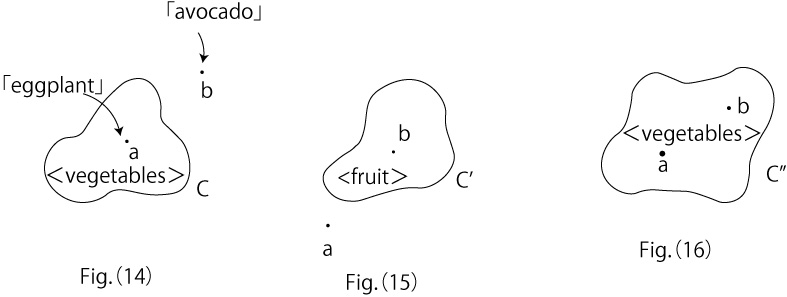

In Fig.(14), we correspond complex number a to `eggplant’ and b to `avocado’, with the inside of C considered as the Set of Vegetables.
Eq.6 and Eq.7 show that `eggplant’ belongs to the Set of Vegetables whereas `avocado’ doesn’t belong to it.
In Fig.(15), we consider the inside of C’ as the Set of Fruits.
Eq.8 and Eq.9. show that `avocado’ belongs to the Set of Fruits whereas `eggplant’ doesn’t belong to it.
Fig.(16) shows that by considering `avocado’ as a vegetable, the Set of Vegetables’ was formed inside the closed curve C’’, with both of `eggplant’ and `avocado’ belonging to the Set of Vegetables’.
Eq.8~Eq.11 describe the extremely important theorem in complex analysis.
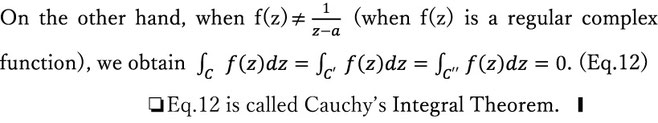
Here, I’d like to think about what Eq.12 means when f(z)=z.
Let us imagine the following daily situation.
-A businessman works around with his products.
He strived, but couldn’t sell any. Suppose he had started from the point A (the office) on the closed curve C surrounding the origin O and came back to the starting point A.
In that case, although his physical work could undoubtedly give some positive value, his economic work ended up in nothing (=0).
If his boss yelled to him `You’ve walked around in vain all day long!’, his semantic work also would be nothing (=0).
We could describe the situation above with mathematics as follows.

This is a mathematical metaphor showing in advance the close relationship between complex number and `meaning’.

The equation above means that the work of the businessman (=the total sum of zdz) who produced no profit should be reduced to nothing (=0), because every point z on the closed curve C is clothed with the `meaning’ related to `the profit for the company’.
Nonetheless…Even if he made a lot of profit, the semantic work (Ws) of this businessman would be nothing (=0). We’ll discuss this paradox later in this book.
In this mathematical metaphor, the circulation movement of the businessman is described by the closed curve C, on the real plane from the physical viewpoint and on the complex viewpoint from the semantic viewpoint.
The close relationship between complex number and meaning will become clearer while reading this book.
To tell the truth…
On the moment I encountered the notion of Circulation Integral along the closed curve C on the complex plane, I was given two different sorts of inspirations at the same time.
※The closed curve C is a Set itself.
※※Human beings keep going round a specific meaning (=singularity a or O). But in short, that `meaning’ is `meaningless’.
In this section, we focus on the idea ※ with only a little bit of suggestion about ※※. Yet it is not too much to say that this `going round’ (circulation movement) is the most important subject of this book.
For this very reason, ※※ contains a lot of difficult problems so we limit our discussion to ※ in this section.
※※ will be handled later, in relation to quantum mechanics.
Anyway…
Just as I mentioned before, even if someone insists `Avocado is a vegetable!’, I would neither get hostile to them nor get into a panic myself.
For I’m equipped with the ability to follow the rules required by others and the society (i.e. the ability to count the number).
Psychotics, however, consider that kind of situation as something terribly serious.
Here, I’d like to show an equation extremely important. This is called Cauchy’s Integral Expression, which is described as follows.
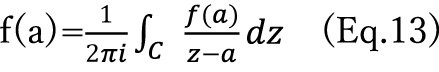
In the equation above, z is a point on the closed curve C; a is a point inside the closed curve C; f(z) is a Regular complex function.
The generalized proof of the formula above is extremely complicated, so we give here only a specific proof about f(z)=z.
Anyway, I think that’s useful enough because we need only one Regular complex function: f(z)=z in this book.